Eksploracja tekstu transkrypcji wypowiedzi kandydatów na prezydenta we wstępnych debatach prezydenckich w USA w 2016 r.
Dane
Zestaw danych zawiera transkrypcje każdej Debaty Demokratycznej i Republikańskiej, która odbyła się w pierwszym sezonie 2016 r.
- Demokraci: 5
- Republikanie: 17
Liczba wypowiedzi
- Demokraci: 1771
- Republikanie (główne debaty): 3251
- Republikanie (wszystkie debaty): 3997
Kandydaci
Democratic
- Chafee: Former Governor Lincoln Chafee (RI)
- Clinton: Former Secretary of State Hillary Clinton
- O’Malley: Former Governor Martin O’Malley (MD)
- Sanders: Senator Bernie Sanders (VT)
- Webb: Former Senator Jim Webb (VA)
Republican
- Bush: Former Governor Jeb Bush (FL)
- Carson: Ben Carson
- Cruz: Senator Ted Cruz (TX)
- Kasich: Governor John Kasich (OH)
- Paul: Senator Rand Paul (KY)
- Rubio: Senator Marco Rubio (FL)
- Trump: Donald Trump
- Walker: Governor Scott Walker (WI)
Republican (Undercard ONLY)
- Gilmore: Former Governor Jim Gilmore (VA)
- Graham: Senator Lindsey Graham (SC)
- Jindal: Governor Bobby Jindal (LA)
- Pataki: Former Governor George Pataki (NY)
- Perry: Former Governor Rick Perry (TX)
- Santorum: Former Senator Rick Santorum (PA)
- Republican (Main AND Undercard)
- Christie: Governor Chris Christie (NJ)
- Fiorina: Carly Fiorina
- Huckabee: Former Governor Mike Huckabee (AR)
Ponieważ kandydatów z ramienia partii republikańskiej było bardzo dużo, debaty zostały podzielone na dwie części: Debaty główne (czyli Main) nadawane w czasie wieczorów wyborczych w porze największej oglądalności, oraz debaty „Undercard” nadawane kilka godzin przed debatami głównymi.
W debatach głównych występowali kandydaci główni, natomiast w debatach undercard kandydaci o niższych notowaniach. Do analizy wykorzystane zostały wypowiedzi kandydatów Republikańskich z obydwu części.
Długości wypowiedzi kandydatów
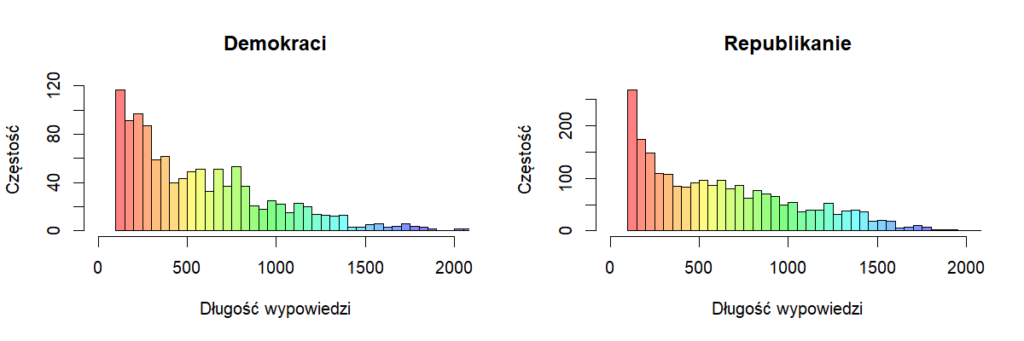
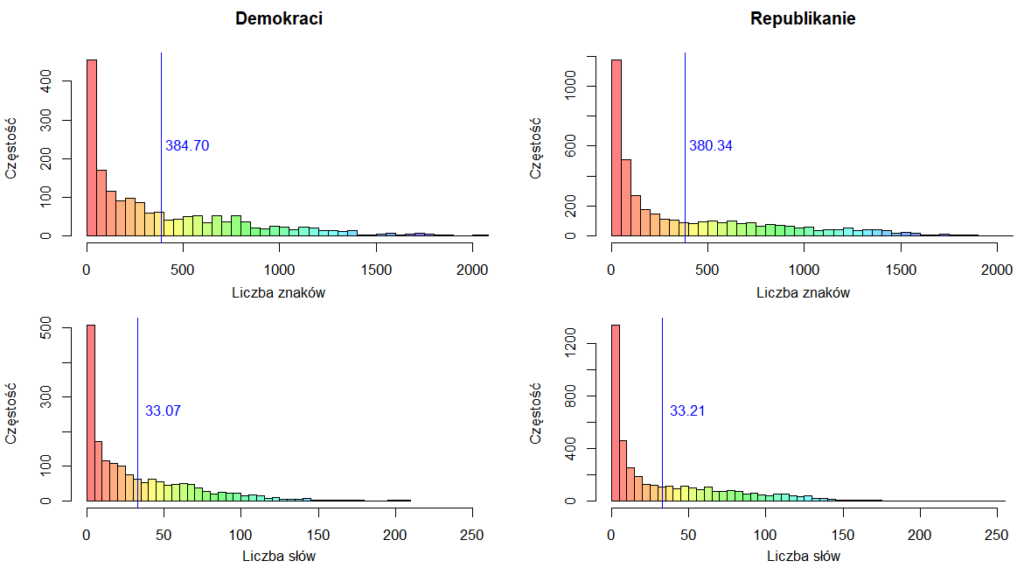
Powyższa ilustracja przedstawia długości wypowiedzi kandydatów względem partii. W górnym rzędzie pokazane są histogramy liczby znaków w wypowiedziach, a w dolnym rzędzie histogramy liczby tokenów po oczyszczeniu i przetworzeniu wypowiedzi (usunięciu znaków, słów ze stoplisty oraz stemmingu). Niebieska linia oznacza wartość średnią. Rozkłady wyglądają podobnie oraz średnia długość wypowiedzi jest dla obu partii praktycznie identyczna i w liczbie znaków i w liczbie tokenów.
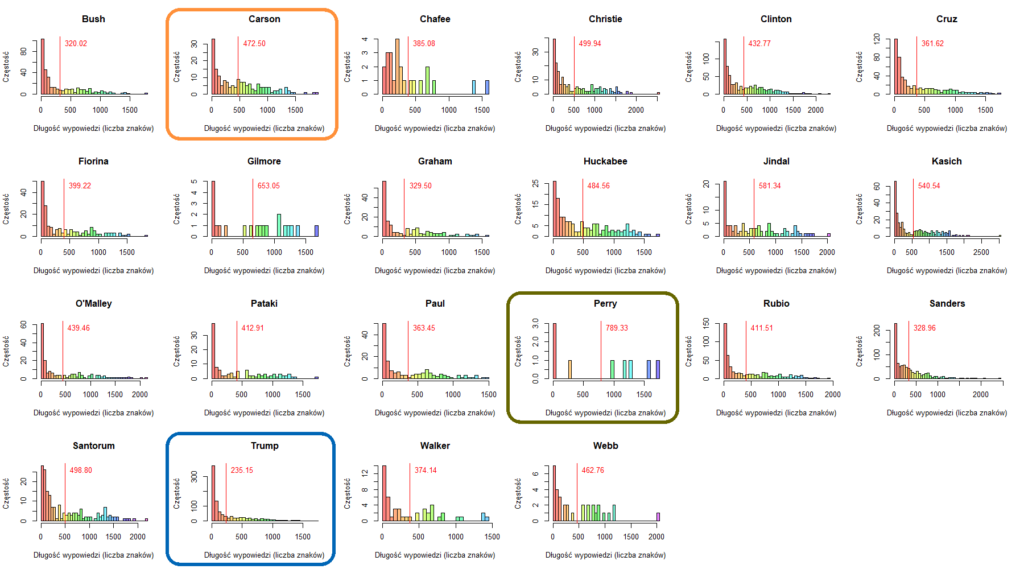
Ilustracja pokazuje rozkłady długości wypowiedzi poszczególnych kandydatów. Czerwona linia oznacza wartość średnią. Widać, że występują duże różnice w liczbie i długości wypowiedzi. Perry miał mniej niż 10 wypowiedzi, ale za to bardzo długich. Po drugiej stronie jest Trump, który miał bardzo dużą liczbę wypowiedzi, ale krótkich. Carson mógłby być przykładem kandydata o średniej liczbie wypowiedzi o średniej długości.
Wypowiedzi kandydatów
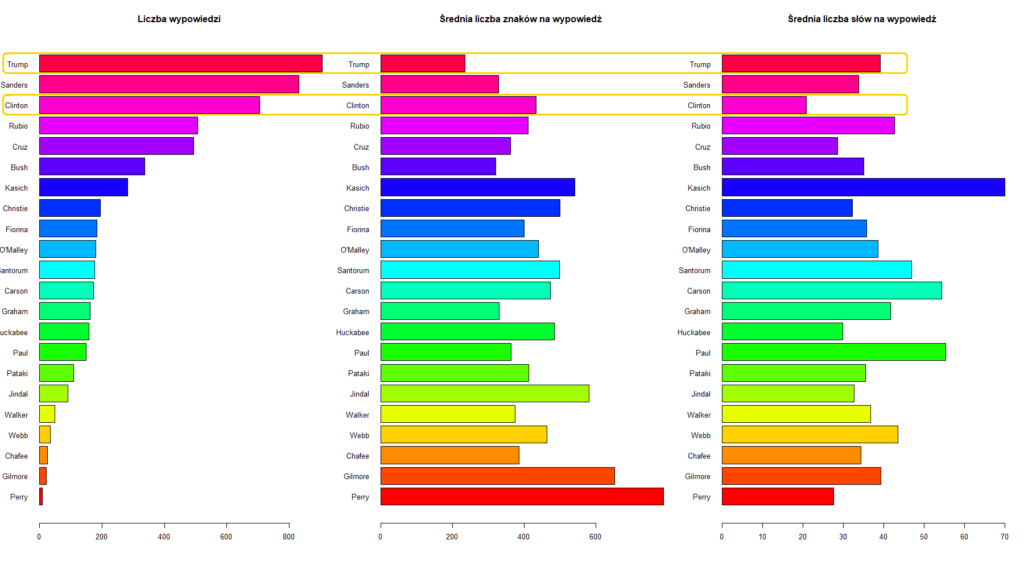 Powyższe wykresy słupkowe pokazują dla każdego kandydata: liczbę wypowiedzi w debatach oraz średnią długość wypowiedzi i średnią liczbą słów w wypowiedzi po usunięciu wyrazów nieznaczących i po stemmingu. Tutaj widać wyraźniej, że Trump miał najwięcej wypowiedzi, ale najkrótszych, a Perry najmniej, ale średnia długość jego wypowiedzi jest największa.
Powyższe wykresy słupkowe pokazują dla każdego kandydata: liczbę wypowiedzi w debatach oraz średnią długość wypowiedzi i średnią liczbą słów w wypowiedzi po usunięciu wyrazów nieznaczących i po stemmingu. Tutaj widać wyraźniej, że Trump miał najwięcej wypowiedzi, ale najkrótszych, a Perry najmniej, ale średnia długość jego wypowiedzi jest największa.
Na tym wykresie można zobaczyć interesującą zależność porównując wypowiedzi Donalda Trumpa – pierwszy od góry i Hillary Clinton – trzeci rząd od góry. Porównując średnią długość wypowiedzi w liczbie znaków, Clinton ma dużo dłuższe wypowiedzi (prawie dwukrotnie), ale po usunięciu wyrazów nieznaczących, ta tendencja się odwraca.
Chmury wyrazów
Demokraci
 Chmury wyrazów używanych w wypowiedziach przez kandydatów obu partii. Obie partie używają najwięcej słów: „people”, „will”, „know”, „country”. Demokraci używają częściej słów: „think”, „well”, a Republikanie: „going”, „need”.
Chmury wyrazów używanych w wypowiedziach przez kandydatów obu partii. Obie partie używają najwięcej słów: „people”, „will”, „know”, „country”. Demokraci używają częściej słów: „think”, „well”, a Republikanie: „going”, „need”.
Republikanie
Analiza sentymentu
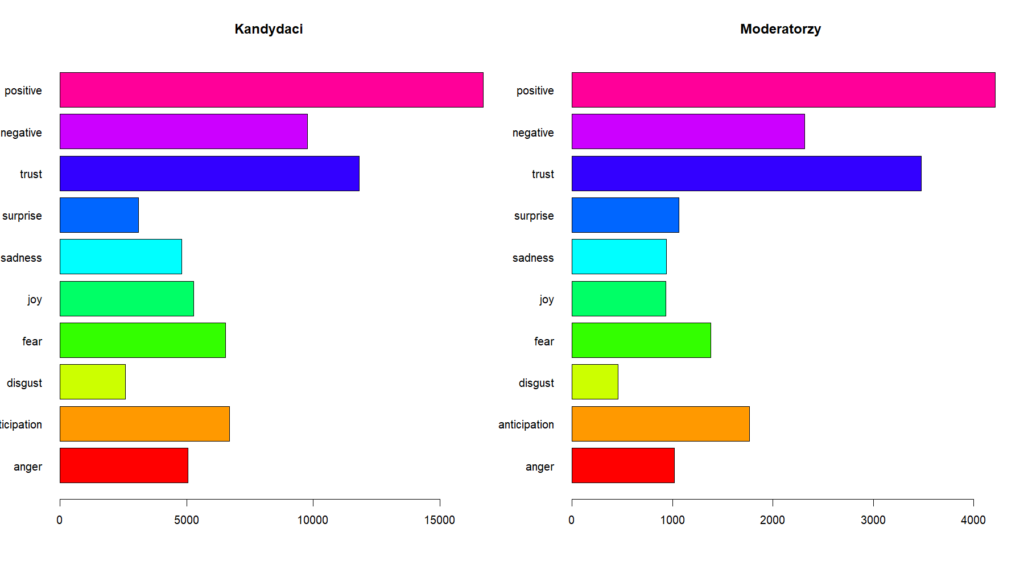
Analiza sentymentu pokazała, że zdecydowana większość wypowiedzi kandydatów obu partii ma charakter pozytywny. Rozkład klasyfikacji wypowiedzi pod kątem zabarwienia emocjonalnego jest w zasadzie bardzo podobny dla obu partii.
Interesowało mnie także porównanie rozkładów występowania emocji w wypowiedziach kandydatów i prowadzących debaty. Spodziewałem się innego rozkładu dla prowadzących ze względu na inny charakter ich wypowiedzi czyli głównie pytania, podziękowania za wypowiedź i komentarze. Jednak wyniki są względnie podobne.
Klasyfikacja
- Partiami: demokratyczna vs republikańska
- KNN (k-Nearest Neighbors)
- Odrzuciłem wypowiedzi krótkie (len > 100 char)
- Usunąłem rzadkie tokeny z TDM (sparseThr <- 0.75)
- Podział na zbiór uczący i testowy 70% : 30%
 Klasyfikacja pod kątem przynależności do partii kandydata od danej wypowiedzi metodą k-najbliższych sąsiadów. Krótkie wypowiedzi zostały odrzucone. Zbiór uczący i testowy podzielone w stosunku 70:30% i zredukowałem wymiarowość usuwając rzadkie słowa.
Klasyfikacja pod kątem przynależności do partii kandydata od danej wypowiedzi metodą k-najbliższych sąsiadów. Krótkie wypowiedzi zostały odrzucone. Zbiór uczący i testowy podzielone w stosunku 70:30% i zredukowałem wymiarowość usuwając rzadkie słowa.
Wyniki klasyfikacji
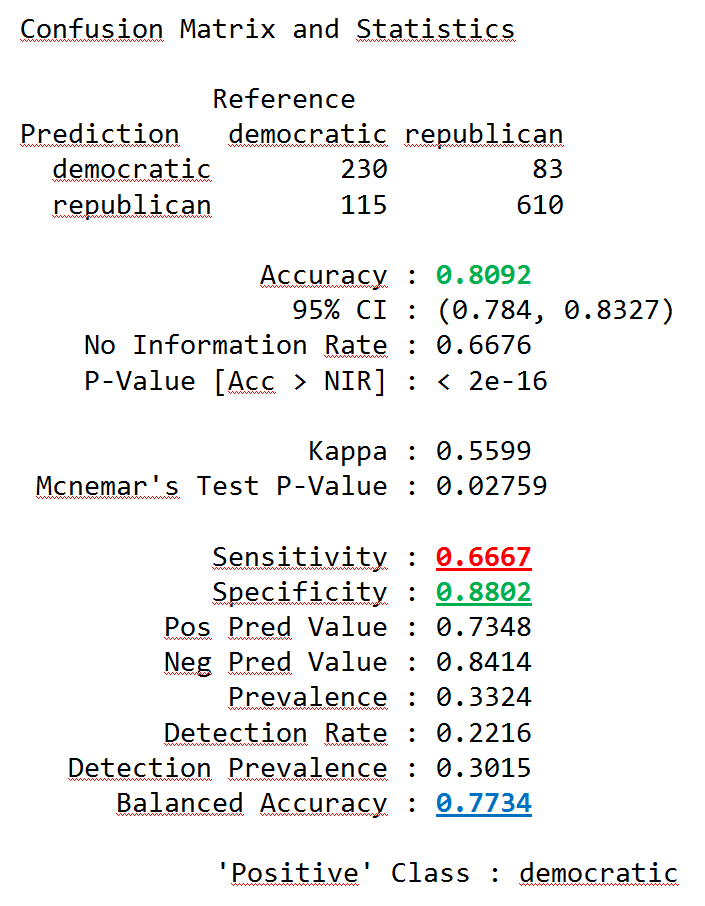
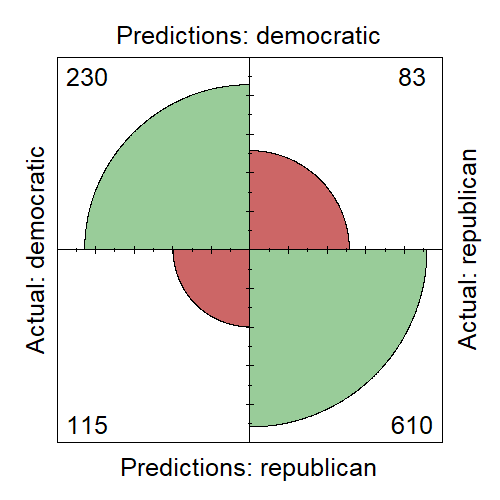
 Dokładność wynosiła ok 81%. A zbalansowana ze względu na różnice w liczności klas dokładność wyniosła ok 77%. Macierz błędów przedstawiona jest w tabelce. Na zielono zaznaczone są poprawne klasyfikacje, na czerwono błędne. Dobra jest wartość specyficzności 88%. Jako klasę dodatnią przyjąłem tutaj demokratów, co oznacza to, że zdolność wykrywania wypowiedzi republikanów wynosi 88%. Czułość jest gorsza – 66.67%, co oznacza, że dwa z trzech tekstów demokratów są klasyfikowane poprawnie.
Dokładność wynosiła ok 81%. A zbalansowana ze względu na różnice w liczności klas dokładność wyniosła ok 77%. Macierz błędów przedstawiona jest w tabelce. Na zielono zaznaczone są poprawne klasyfikacje, na czerwono błędne. Dobra jest wartość specyficzności 88%. Jako klasę dodatnią przyjąłem tutaj demokratów, co oznacza to, że zdolność wykrywania wypowiedzi republikanów wynosi 88%. Czułość jest gorsza – 66.67%, co oznacza, że dwa z trzech tekstów demokratów są klasyfikowane poprawnie.
Klasyfikacja – Kandydaci
Próba klasyfikacji wypowiedzi dla wszystkich kandydatów indywidualnie. Krótkie wypowiedzi zostały usunięte, a zbiór podzielony na uczący i testowy w stosunku: 70%:30%. Macierz błędu dla tej klasyfikacji przedstawiona jest poniżej. Na zielono zaznaczone są poprawne klasyfikacje. Dokładność klasyfikacji wynosiła to ok 51%. Jest to wartość znacznie niższa niż w przypadku klasyfikacji wypowiedzi do dwóch klas, jednak biorąc pod uwagę dużą liczbę kandydatów jest dobrym wynikiem.
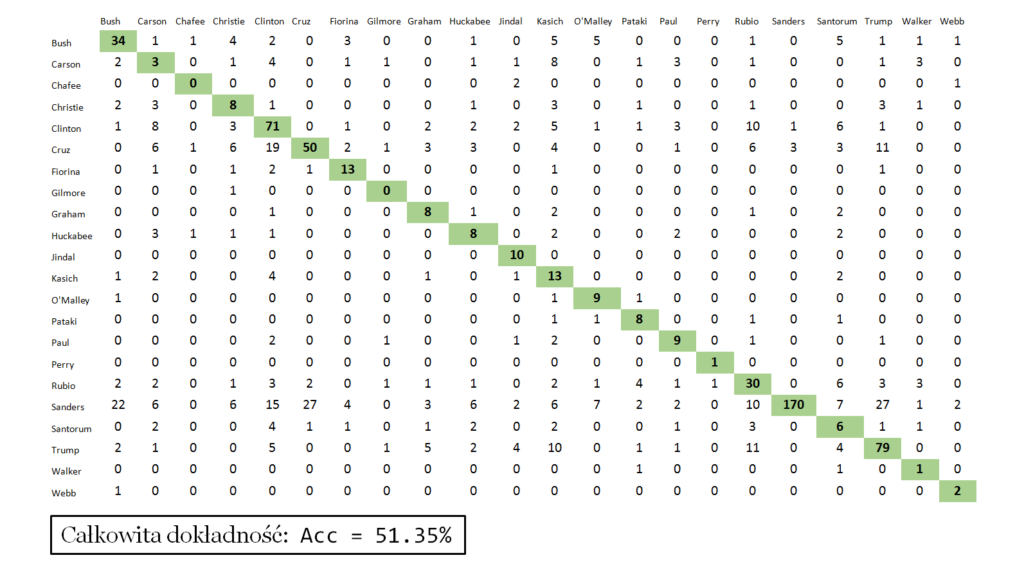
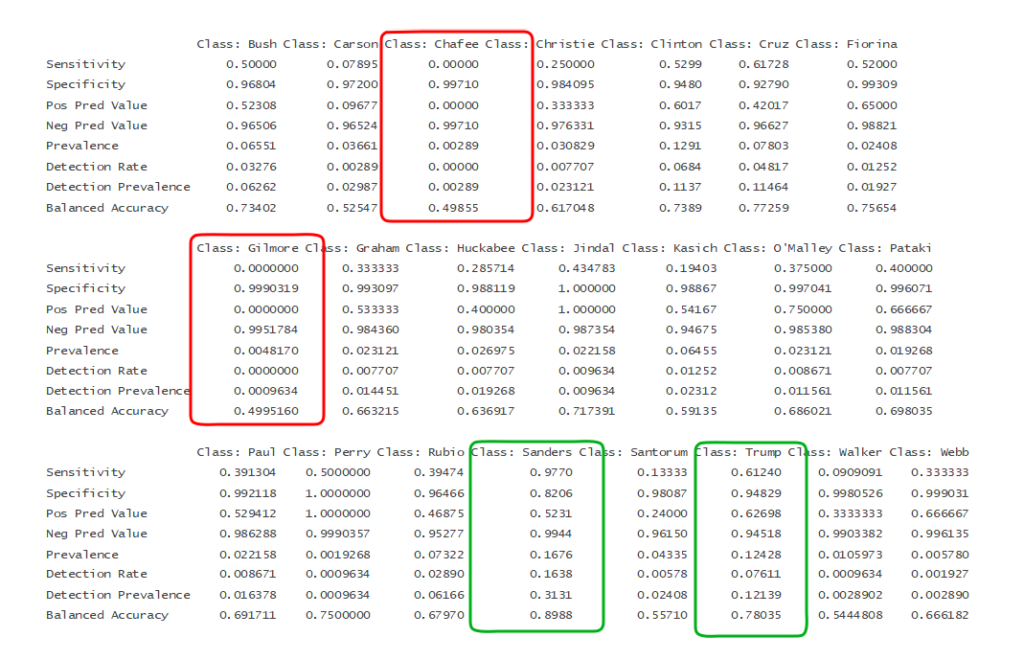 Miary jakości klasyfikacji dla każdej klasy z osobna. Są klasy dla których klasyfikator daje bardzo złe wyniki np. Chafee czy Gilmore – są to klasy mało liczne, ale są też klasy takie jak: Sanders czy Trump gdzie klasyfikacja jest relatywnie dobra – te klasy są liczne.
Miary jakości klasyfikacji dla każdej klasy z osobna. Są klasy dla których klasyfikator daje bardzo złe wyniki np. Chafee czy Gilmore – są to klasy mało liczne, ale są też klasy takie jak: Sanders czy Trump gdzie klasyfikacja jest relatywnie dobra – te klasy są liczne.



 polski
polski English
English