Termin Multilayer Kernel Machines (MKMs) został wprowadzony w 2012 roku w pracy doktorskiej Youngmin Cho pisanej pod kierunkiem Prof. Lawrenca Saul (1). Autor zaproponował nowy model hierarchiczny oparty o przekształcenia jądrowe, czerpiący z wcześniejszych badań nad rodziną jąder arc-cosinusowych (2). Ideą badań i rozwoju MKMs była chęć obejścia słabości maszyn wektorów nośnych (ang. Support Wektor Machines, SVM) oraz wykorzystania zalet systemów głębokich. Realizacja MKMs bazowała na koncepcji połączenia technik nienadzorowanej redukcji wymiarowości i nadzorowanego wyboru cech z wielowarstwowymi jądrami arc-cosinusowymi. Indywidualne kroki w tej procedurze korzystają z dobrze znanych i szeroko stosowanych metod, jednak ich połączenie w zaproponowanej metodzie tworzenia MKMs było nowatorskie.
Zasada działania i uczenia się Multilayer Kernel Machines
Multilayer Kernel Machines są trenowane przy wykorzystaniu kombinacji metod uczenia nadzorowanego i nienadzorowanego. U podstaw ich działania leży rekursywnie przeprowadzana iteracja trzech procesów:
- „trik jądrowy” polegający na nieliniowej transformacji (najlepiej przez jądra arc-cosinusowe)
- nienadzorowaną redukcję wymiaru poprzez jądrową analizę składowych głównych Kernel Principal Component Analysis (KPCA)
- oraz nadzorowany wybór cech.
Cykl ten jest wielokrotnie powtarzany w celu skonstruowania MKM.
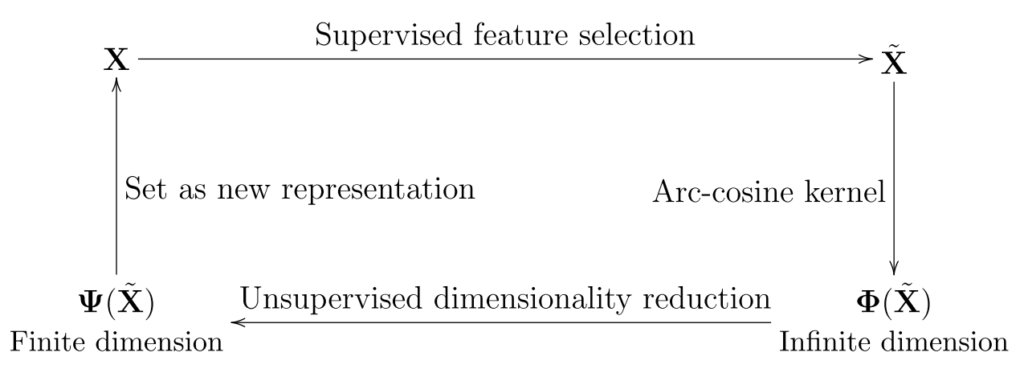
Z pracy: (1)
Powyższy schemat przedstawia podstawową koncepcję konstrukcji Multilayer Kernel Machines. Dane wejściowe X są filtrowane w procesie nadzorowanej selekcji cech w ten sposób, aby zawierały wyłącznie cechy powiązane z informacją klasyfikowaną. Otrzymane dane X’ są poddawane przetwarzaniu przez jądra arc-cosinusowe tworzące nieskończenie wymiarową reprezentację Φ(X’). W kolejnym kroku następuje nienadzorowana redukcja wymiarowości Φ(X’) w przestrzeni cech i otrzymywana jest skończeniewymiarowa reprezentacja Ψ(X’). Następnie Ψ(X’) podawane jest na wejście i cały cykl powtarzany jest wielokrotnie np. L razy w celu utworzenia L –warstwowej MKM. Na samym końcu procedury, cechy ostatniej warstwy podawane są na wejście jakiegoś klasyfikatora (jak np. k-NN lub SVM) w celu podjęcia końcowej decyzji.
Procedurę uczenia Multilayer Kernel Machines opisuje następujący pseudokod:

Nienadzorowana redukcja wymiarowości – Kernel Principal Components Analysis (KPCA)
W Multilayer Kernel Machines głębokie uczenie realizowane jest przez iteracyjne powtarzanie na kolejnych warstwach procedury KPCA, przedstawionej w 1998 w pracy (3). Dane wyjściowe (cechy w postaci składowych głównych) z KPCA z jednej warstwy stanowią wejście do KPCA w warstwie następnej. Składowe te nie są jednak przenoszone bezpośrednio. Usuwane są składowe, które zostały uznane za nieinformacyjne, czyli niezwiązane z informacją wpływającą na klasyfikację. W zasadzie wszystkie nieliniowe jądra mogą zostać użyte przy analizie składowych głównych w MKMs, ale rdzenie arc-cosinusowe wydają się być najlepszym wyborem ponieważ odzwierciedlają obliczenia w wielkich sieciach neuronowych.
Analiza składowych głównych (PCA) jest ortogonalną transformacją systemu współrzędnych opisującego dane. Często wykonywana jest poprzez rozwiązanie równania znajdującego wartości i wektory własne, a czasami przy wykorzystaniu algorytmów iteracyjnych. W przypadku dużej (lub nieskończonej jak w przypadku MKM) wymiarowości danych rozwiązaniem może być wykorzystanie jąder w metodzie Kernel Principal Components Analysis KPCA.
KPCA przebiega zgodnie z następującym algorytmem. Na początku utworzona zostaje macierz Kij=(k(xi,xj))ij. Następnie rozwiązywane jest równanie własne poprzez diagonalizację macierzy K i normalizowane są współczynniki rozwinięcia αn wektorów własnych poprzez wiąz: λn(αn·αn )=1, gdzie λ oznacza wartości własne macierzy K. W celu wydobycia składowych głównych (odpowiednich dla jądra k) wektora x, obliczane są jego rzuty na wektory własne:
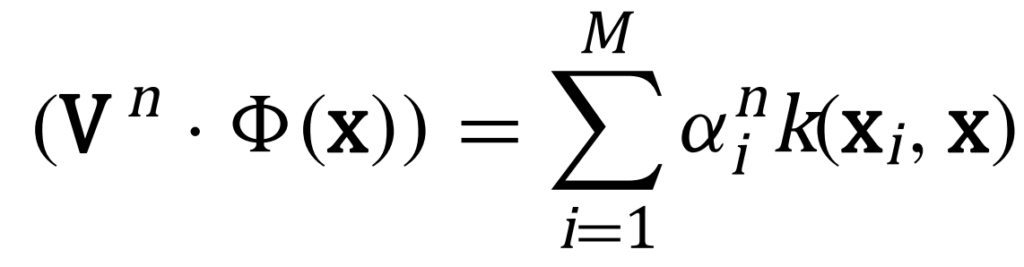
W przypadku jąder arc-cosinusowych procedura ta dokładnie odpowiada standardowej PCA w przestrzeni cech, bez konieczności wykonywania obliczeń w tej przestrzeni.
Wybór cech
W Multilayer Kernel Machines warstwy są uczone poprzez połączenie nadzorowanej metody wyboru cech i nienadzorowanej metody KPCA. Wybór cech ma na celu odrzucenie cech nieinformacyjnych na poziomie każdej warstwy (włączając w to także oryginalne dane wejściowe). Pozwala to skoncentrować nienadzorowane uczenie MKMs na składowych rzeczywiście zawierających informacje o oznaczeniach klas. Ograniczenie cech w każdej warstwie odbywa się w dwóch etapach: poprzez oszacowanie dla cech ich informacji wzajemnej, oraz ich okrojenie w oparciu o walidację krzyżową. Pierwszy etap realizowany jest przez dyskretyzację cech i konstrukcję histogramów warunkowego i marginalnego rozkładu dyskretnych wartości dla klas, a następnie w oparciu o te rozkłady estymowana jest dla każdej cechy informacja wzajemna z oznaczeniem klasy oraz następuje posortowanie cech zgodnie z wartością tego oszacowania (4). W drugim kroku uwzględniając wyłącznie w pierwszych cech zgodnie z tym uporządkowaniem, obliczane są wskaźniki błędu klasyfikatora k-NN (k-najbliższych sąsiadów) w oparciu o odległość Euklidesową w przestrzeni cech. Wartości błędu obliczane są na losowym zestawie walidacyjnym próbek, dla różnych wartości k i w i zapamiętywane są wartości optymalne. Optymalna wartość w określa liczbę cech o zawartości informacyjnej która będzie przekazana do następnej warstwy. Z tego wynika, że wartość w określa szerokość warstwy.
Klasyfikacja – nauka metryki
W pracy (1) cechy na wyjściu ostatniej warstwy klasyfikowane były przy wykorzystaniu odmiany klasyfikatora k-NN. Autor użył klasyfikacji Large Margin Nearest Neighbor (LMNN) przedstawionej w pracy (5), a jako miarę odległości wykorzystał metrykę Mahalanobisa. Odległość Mahalanobisa jest zgodnie z formalizmem matematycznym pseudometryką ponieważ spełnia wszystkie właściwości metryk z wyjątkiem warunku rozróżnialności: D(xi ,xj )=0 ⇔ xi=xj. Odległość Mahalonobisa opisuje się wzorem:
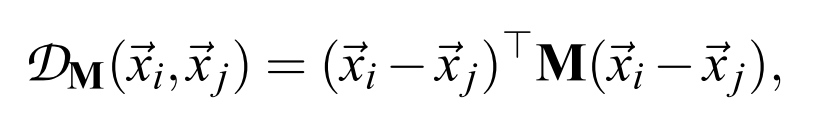
gdzie oryginalnie macierz M jest odwrotnością macierzy kowariancji.
Matematyczne podstawy rdzeni arc-cosinusowych
W pracy (2) opublikowanej jako artykuł z konferencji Neural Information Processing Systems 2009, Youngmin Cho i Lawrence K. Saul zaproponowali nową rodzinę funkcji jądrowych (rdzeni) odzwierciedlających obliczenia w wielkich sieciach neuronowych oraz przedstawili metodę uczenia Multilayer Kernel Machines przy wykorzystaniu tych funkcji. Praca zawierała część materiału z pracy doktorskiej Youngmin Cho pisanej pod kierunkiem Prof. Lawrenca Saul (1).
Autorzy zaprezentowali rodzinę funkcji jądrowych (rdzeni) pozwalających na obliczenie podobieństwa dwóch wektorów x, y ∈ Rd. Reprezentacja funkcji w postaci całkowej wygląda następująco:
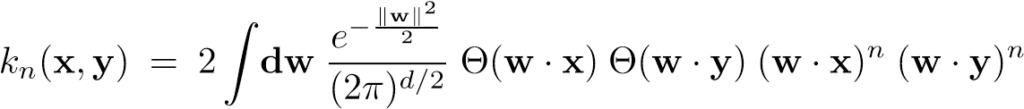
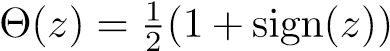
Analityczne oszacowanie tej całki (2) pozwala na zapis funkcji w postaci:
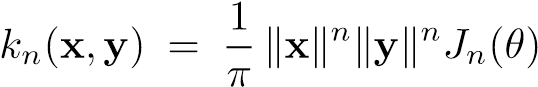
czyli iloczynu składowej zależnej od modułów obu wektorów, oraz składowej Jn(θ) zależnej od kąta pomiędzy nimi w sposób:
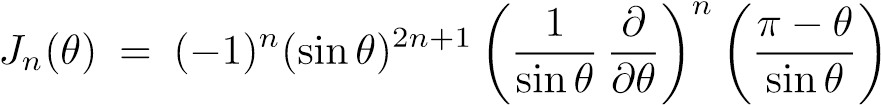
gdzie θ oznacza kąt pomiędzy wektorami x i y:
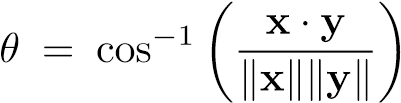
Zaproponowane rdzenie są nazywane zgodnie z sugestią autorów rdzeniami arcus-cosinusowymi (ang. Arc-cosine kernels) ze względu na postać rdzenia zerowego rzędu:
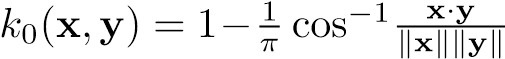
Rdzenie wyższych rzędów z tej rodziny mają bardziej skomplikowaną składową opisującą zależność kątową Jn(θ) np.:
J1(θ)=sinθ + (π − θ)cosθ lub J2(θ)=3sinθ cosθ + (π − θ)(1 + 2cos2 θ).
Dodatkowo, ponieważ iloczyn skalarny wektorów wyjściowych f(x) i f(y) z jednowarstwowej sieci o m jednostkach wyjściowych i funkcji aktywacji postaci gn(z) = Θ(z)zn, rzędu n, opisuje się równaniem:
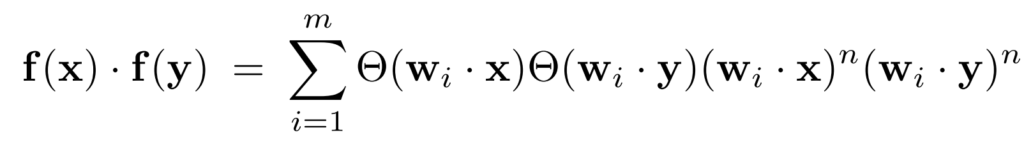
gdzie, wi oznacza i-ty rząd macierzy wag, a x i y to wektory cech na wejściu, to z tego powodu, można jądra arc-cosinusowe zgodnie z ich reprezentacją w formie całkowej, interpretować jako iloczyn skalarny wektorów cech przepuszczonych przez nieskończoną (w granicy m→∞) jednowarstwową sieć progową. Jest to cecha, która odróżnia jądra arc-cosinusowe od jąder wielomianowych czy RBF (gaussowskich). Rdzenie arc-cosinusowe posiadają jeszcze jedną ważną cechę, mianowicie nie mają żadnych parametrów wymagających określenia (np. na zbiorze walidacyjnym) takich jak np. szerokość w rdzeniach RBF.
Rdzenie można rozumieć jako nieliniowe mapowanie wejścia x do wektora cech Φ(x). Jednocześnie rdzeń jest iloczynem skalarnym w wytworzonej przestrzeni cech: k(x,y) = Φ(x)·Φ(y). Skoro ta funkcja odzwierciedla działanie jednowarstwowej sieci, to funkcja postaci:
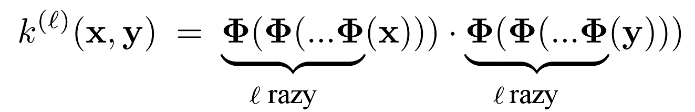
odzwierciedla przetwarzanie przez wielowarstwową sieć progową. Dla rdzeni arc-cosinusowych, zgodnie z analityczną postacią oszacowania całki, będzie wyglądała następująco:
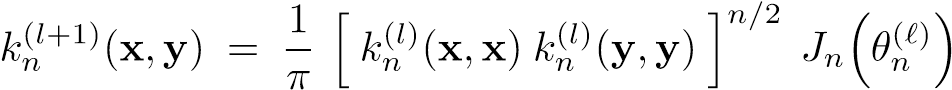
gdzie θn(l) jest kątem pomiędzy projekcjami x i y do przestrzeni cech wytworzonej przez l-krotne złożenie. Jest to równanie rekurencyjne o podstawie (l=0) postaci:
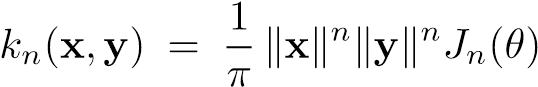
jednak zgodnie z (1) łatwe do wyliczenia. W równaniu rekurencyjnym, autorzy dla uproszczenia przyjęli ten sam rząd n (liczbę jednostek) w każdej warstwie, jednak w praktyce można stosować różne rzędy rdzeni dla różnych warstw.
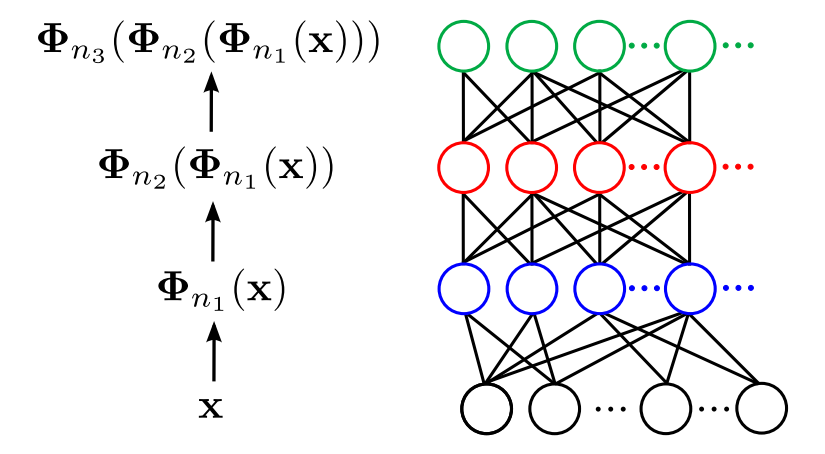
Rys. z pracy (1) pokazujący modelowanie wielowarstwowej sieci neuronowej poprzez składanie rdzeni arc‑cosinusowych.
To, że składanie jąder arc-cosinusowych prowadzi do funkcji nie będącej członkiem oryginalnej rodziny, także jest specyficzną cechą tych funkcji odróżniającą je od innych rdzeni. Np. składanie rdzeni wielomianowych prowadzi do utworzenia nowego rdzenia wielomianowego wyższego rzędu, a w składanie jąder RBF spowoduje powstanie jądra RBF, ale o innej wariancji.
W pracy (1) autorzy rozszerzyli koncepcję składania jąder arc-cosinusowych o mnożenie i uśrednianie.
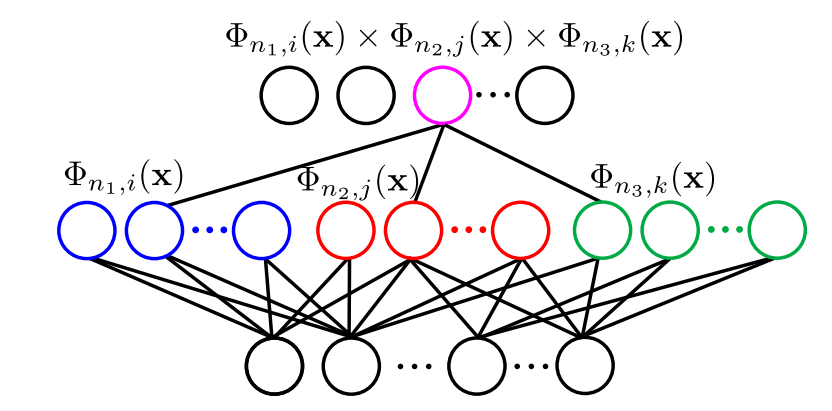
Wielowarstwowa sieć neuronowa modelowana przez mnożenie jąder arc-cosinusowych. Φn,m oznacza m-tą cechę wprowadzaną przez jądro arc-cosinusowe stopnia n. Różne kolory w warstwach pośrednich oznaczają różne nieliniowe odwzorowania generowane przez odpowiadające im jądra.
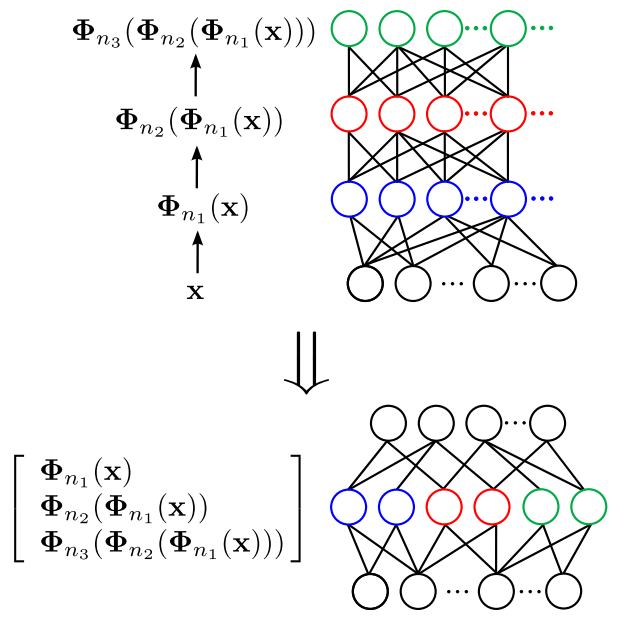
Wielowarstwowa sieć neuronowa modelowana przez uśrednianie. Odwzorowania nieliniowe w różnych warstwach wielowarstwowego jądra (na górze) są łączone jako reprezentacja pojedynczej cechy (na dole) przez uśrednianie rdzeni.
Jądra arc-cosinusowe, a Multilayer Kernel Machines
Powstanie Multilayer Kernel Machines było zainspirowane badaniami nad rdzeniami arc-cosinusowymi. Poniższy schemat porównuje dwa systemy: SVM z jądrami arc-cosinusowymi i MKMs.
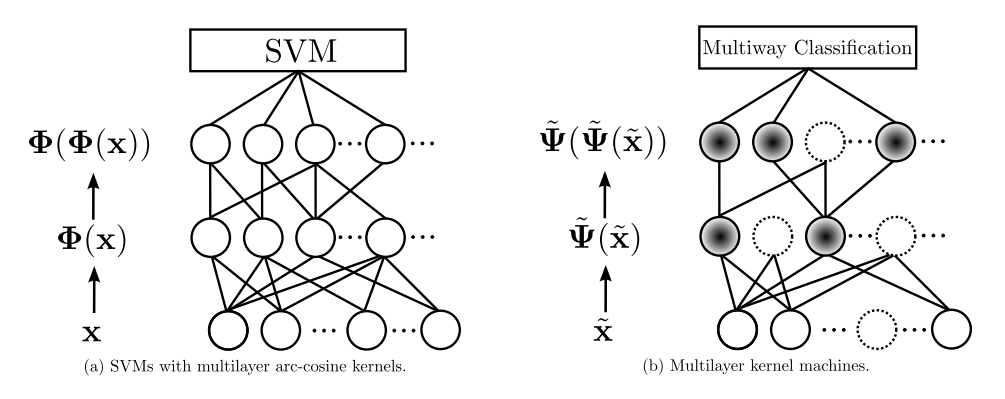
Oba modele wykorzystują rdzenie arc-cosinusowe, w każdej warstwie do przetwarzania danych na wejściu, które są następnie przekazywane do następnej warstwy, aż do końcowej reprezentacji. W przypadku wielowymiarowych jąder arc-cosinusowych końcowe cechy są podawane na wejście klasyfikatora SVM. Ale w przypadku MKMs, miejsce mają dodatkowe operacje modyfikujące cechy na poziomie każdej warstwy. Przede wszystkim MKMs redukują wymiarowość reprezentacji jądrowej, co powoduje zmniejszenie szumu i bardziej zwartą reprezentację danych. Zmiana nieskończeniewymiarowej reprezentacji w skończeniewymiarową ma dwie zalety.
- Po pierwsze, pozwala na ocenę związku cech z informacją dotyczącą klasyfikacji, dzięki czemu część cech może być usunięta. Na powyższym schemacie usuwanie cech symbolizowane jest przez okręgi rysowane przerywaną linią. W nieskończeniewymiarowej przestrzeni jądrowej (jak w przypadku modelu „rdzenie arc-cosinusowe + SVM”, po lewej stronie) taka ocena nie byłaby możliwa.
- Po drugie, w przypadku MKMs na ostatniej warstwie można wykorzystać jakikolwiek klasyfikator, ponieważ dzięki redukcji wymiarowości, dane nie są wyrażone w przestrzeni jądrowej cech.
Podsumowanie
Multilayer Kernel Machines są to systemy wykorzystujące architekturę głęboką (wielowarstwową) oraz przekształcenia jądrowe do przestrzeni cech przy wykorzystaniu rdzeni arc-cosinusowych. Uczenie warstw ukrytych MKMs odbywa się dzięki połączeniu w każdej warstwie (kroku iteracji) nienadzorowanej metody redukcji wymiarowości (oryginalnie KPCA) oraz nadzorowanej metody wyboru cech (składowych o zawartości informacyjnej). Na wyjściu MKMs może znajdować się jeden z powszechnie stosowanych klasyfikatorów (oryginalnie LMNN z metryką Mahalanobisa).
Multilayer Kernel Machines zostały zainspirowane wielowarstwowymi jądrami arc-cosinusowymi. Badania nad MKMs, były motywowane tym, że architektura w postaci wielowarstwowych jąder arc-cosinusowych i klasyfikatora SVM na wyjściu, nie jest optymalna ponieważ przekształcenia jądrowe w każdej warstwie mieszają cechy informacyjne z szumem.
W przypadku MKMs, dodanie w każdej warstwie redukcji wymiaru i selekcji wyłącznie cech informacyjnych pod kątem docelowej klasyfikacji, pozwala poddawać dalszemu przetwarzaniu przez kolejną warstwę, tylko wybrane cechy mające wkład w klasyfikację. Dzięki temu w każdej warstwie zachodzi jakby filtrowanie szumu (składowych nie związanych z problemem klasyfikacyjnym rozwiązywanym przez MKM).
Zgodnie z (6), badacze z Microsoftu przedstawili prostszy sposób implementacji MKMs do rozumienia mowy (7), jednak w tym wpisie skoncentrowałem się na oryginalnej interpretacji definiującej MKMs w oparciu o rdzenie arc-cosinusowe.
Bibliografia
- Cho, Youngmin. Kernel Methods for Deep Learning. San Diego: University of California, 2012.
- Kernel Methods for Deep Learning. Youngmin Cho, Lawrence K. Saul. 2009. Neural Information Processing Systems. pp. 342-350.
- Schölkopf, Bernhard, Alexander Smola, and Klaus-Robert Müller. Nonlinear component analysis as a kernel eigenvalue problem. Neural computation 10.5. 1998, pp. 1299-1319.
- Guyon, I. and Elisseeff, A. An introduction to variable and feature selection. Journal of Machine Learning Research 3. 2003, pp. 1157–1182.
- Weinberger, K. Q. and Saul, L. K. Distance metric learning for large margin nearest neighbor classification. Journal of Machine Learning Research, 10. 2009, pp. 207–244.
- Wikipedia. [Online] 2017. https://en.wikipedia.org/wiki/Deep_learning#Multilayer_kernel_machine.
- L. Deng, G. Tur, X. He, and D. Hakkani-Tur. Use of Kernel Deep Convex Networks and End-To-End Learning for Spoken Language Understanding. Proc. IEEE Workshop on Spoken Language Technologies. 2012.
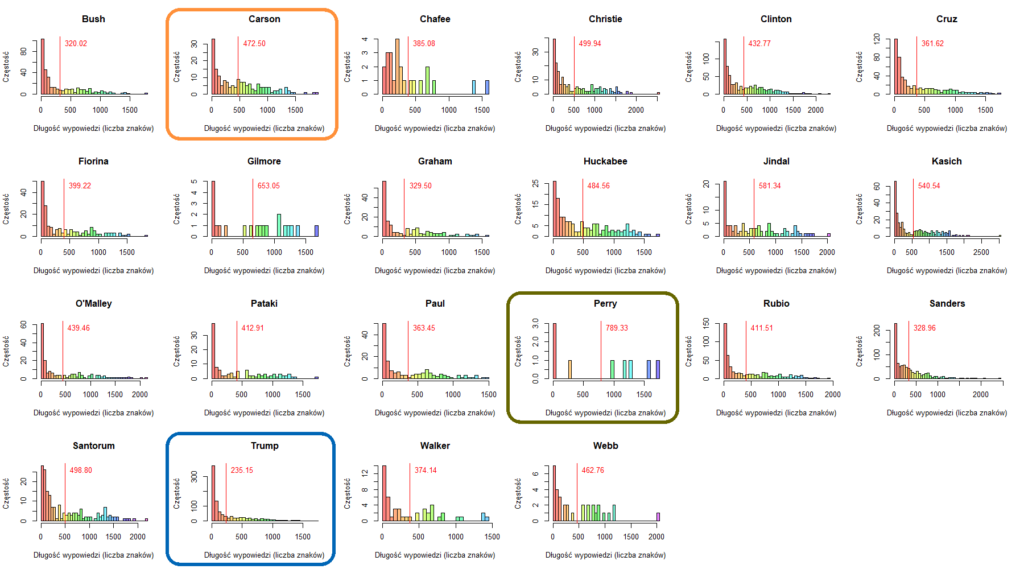
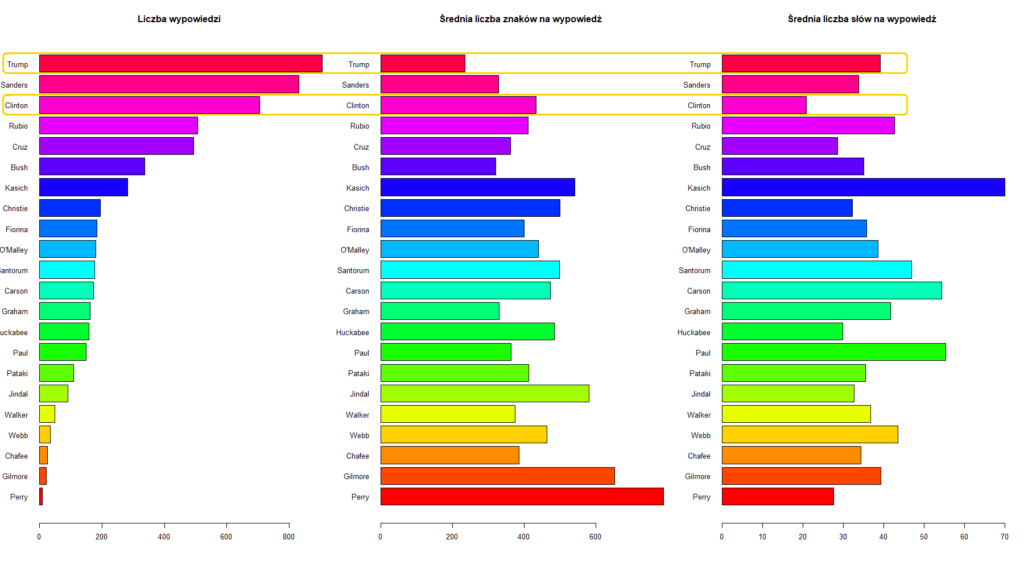 Powyższe wykresy słupkowe pokazują dla każdego kandydata: liczbę wypowiedzi w debatach oraz średnią długość wypowiedzi i średnią liczbą słów w wypowiedzi po usunięciu wyrazów nieznaczących i po stemmingu. Tutaj widać wyraźniej, że Trump miał najwięcej wypowiedzi, ale najkrótszych, a Perry najmniej, ale średnia długość jego wypowiedzi jest największa.
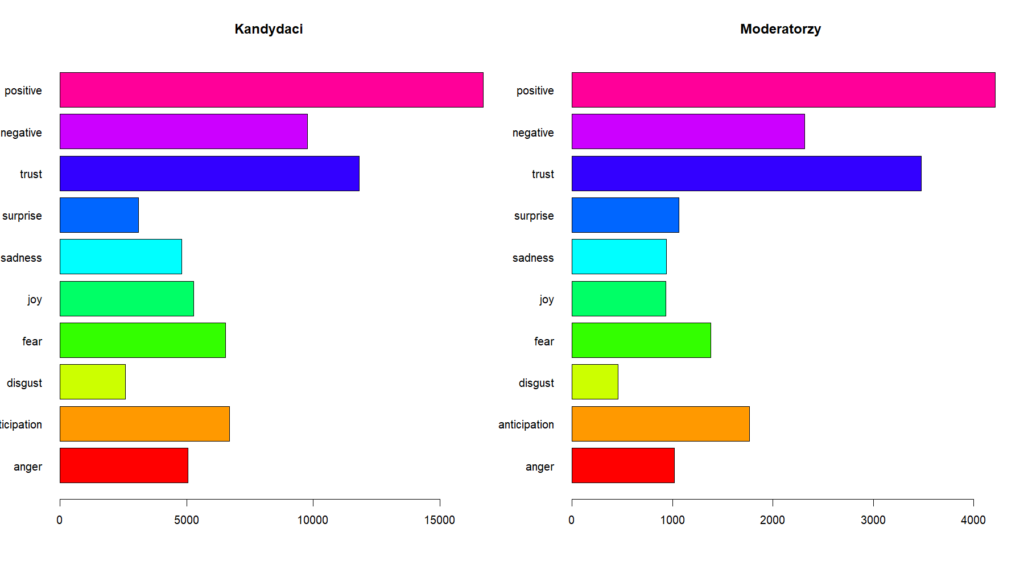
Powyższe wykresy słupkowe pokazują dla każdego kandydata: liczbę wypowiedzi w debatach oraz średnią długość wypowiedzi i średnią liczbą słów w wypowiedzi po usunięciu wyrazów nieznaczących i po stemmingu. Tutaj widać wyraźniej, że Trump miał najwięcej wypowiedzi, ale najkrótszych, a Perry najmniej, ale średnia długość jego wypowiedzi jest największa. Chmury wyrazów używanych w wypowiedziach przez kandydatów obu partii. Obie partie używają najwięcej słów: „people”, „will”, „know”, „country”. Demokraci używają częściej słów: „think”, „well”, a Republikanie: „going”, „need”.
Chmury wyrazów używanych w wypowiedziach przez kandydatów obu partii. Obie partie używają najwięcej słów: „people”, „will”, „know”, „country”. Demokraci używają częściej słów: „think”, „well”, a Republikanie: „going”, „need”.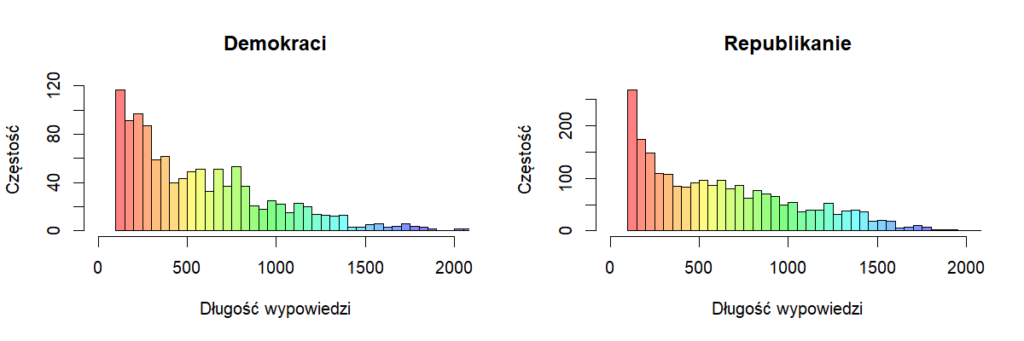 Klasyfikacja pod kątem przynależności do partii kandydata od danej wypowiedzi metodą k-najbliższych sąsiadów. Krótkie wypowiedzi zostały odrzucone. Zbiór uczący i testowy podzielone w stosunku 70:30% i zredukowałem wymiarowość usuwając rzadkie słowa.
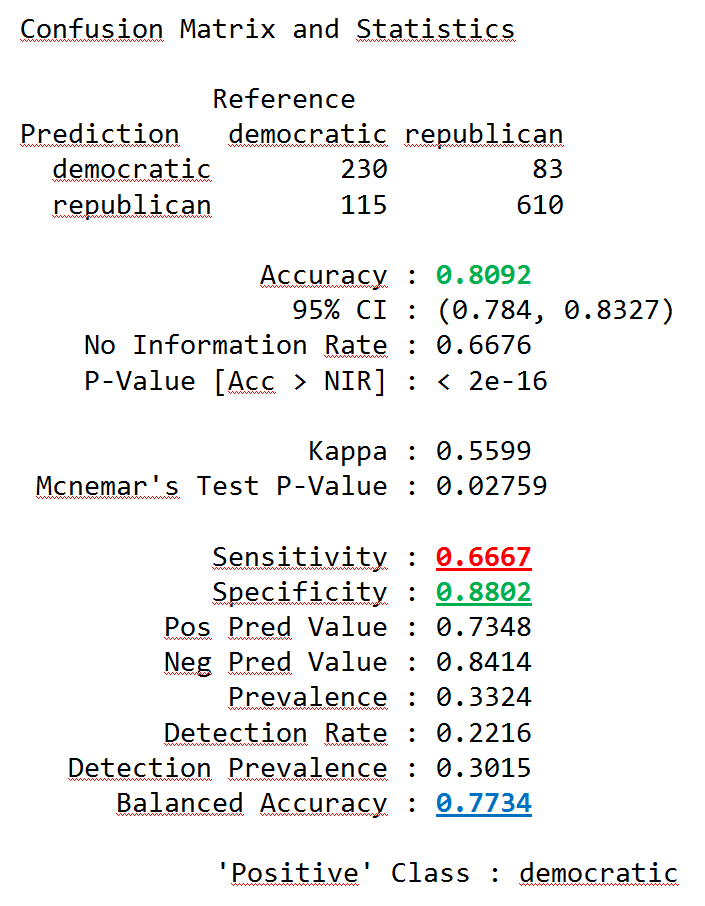
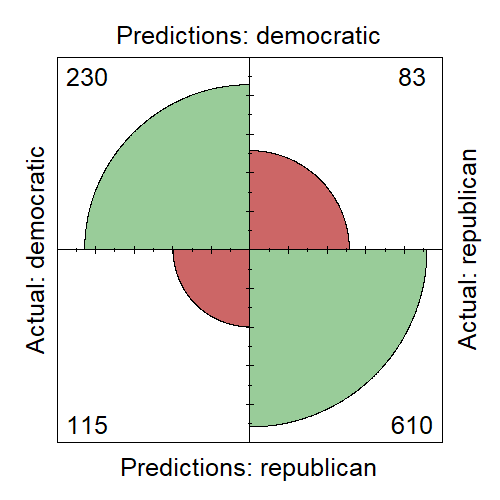
Klasyfikacja pod kątem przynależności do partii kandydata od danej wypowiedzi metodą k-najbliższych sąsiadów. Krótkie wypowiedzi zostały odrzucone. Zbiór uczący i testowy podzielone w stosunku 70:30% i zredukowałem wymiarowość usuwając rzadkie słowa. Dokładność wynosiła ok 81%. A zbalansowana ze względu na różnice w liczności klas dokładność wyniosła ok 77%. Macierz błędów przedstawiona jest w tabelce. Na zielono zaznaczone są poprawne klasyfikacje, na czerwono błędne. Dobra jest wartość specyficzności 88%. Jako klasę dodatnią przyjąłem tutaj demokratów, co oznacza to, że zdolność wykrywania wypowiedzi republikanów wynosi 88%. Czułość jest gorsza – 66.67%, co oznacza, że dwa z trzech tekstów demokratów są klasyfikowane poprawnie.
Dokładność wynosiła ok 81%. A zbalansowana ze względu na różnice w liczności klas dokładność wyniosła ok 77%. Macierz błędów przedstawiona jest w tabelce. Na zielono zaznaczone są poprawne klasyfikacje, na czerwono błędne. Dobra jest wartość specyficzności 88%. Jako klasę dodatnią przyjąłem tutaj demokratów, co oznacza to, że zdolność wykrywania wypowiedzi republikanów wynosi 88%. Czułość jest gorsza – 66.67%, co oznacza, że dwa z trzech tekstów demokratów są klasyfikowane poprawnie.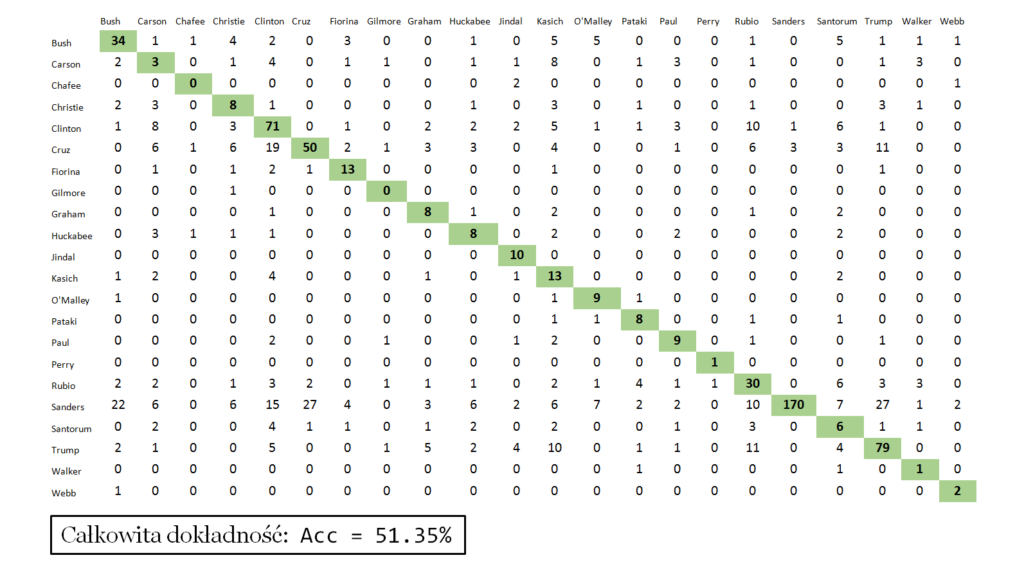
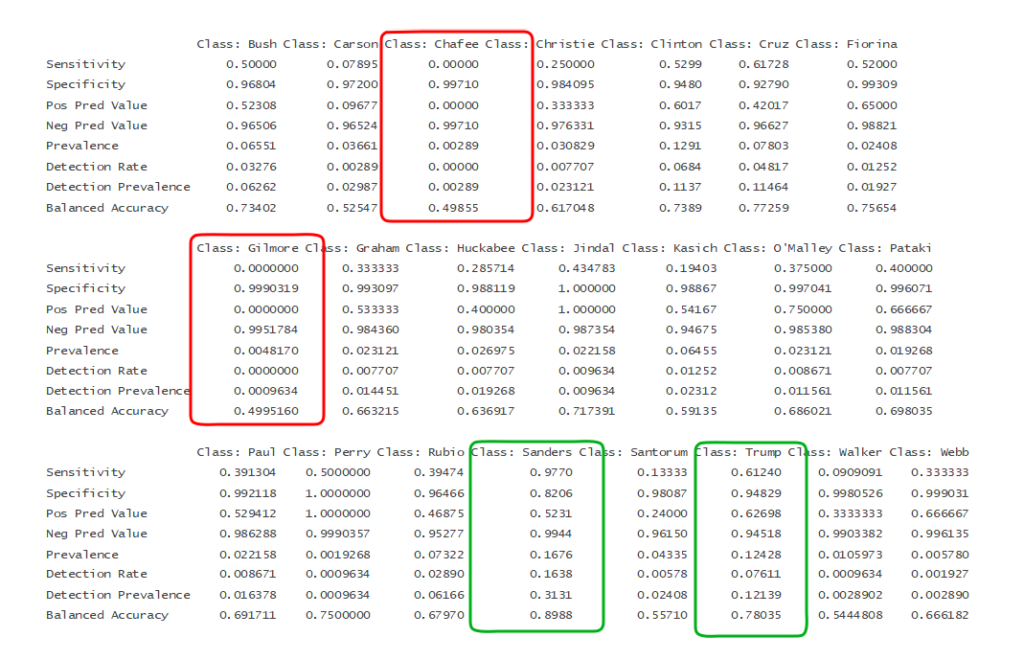 Miary jakości klasyfikacji dla każdej klasy z osobna. Są klasy dla których klasyfikator daje bardzo złe wyniki np. Chafee czy Gilmore – są to klasy mało liczne, ale są też klasy takie jak: Sanders czy Trump gdzie klasyfikacja jest relatywnie dobra – te klasy są liczne.
Miary jakości klasyfikacji dla każdej klasy z osobna. Są klasy dla których klasyfikator daje bardzo złe wyniki np. Chafee czy Gilmore – są to klasy mało liczne, ale są też klasy takie jak: Sanders czy Trump gdzie klasyfikacja jest relatywnie dobra – te klasy są liczne.




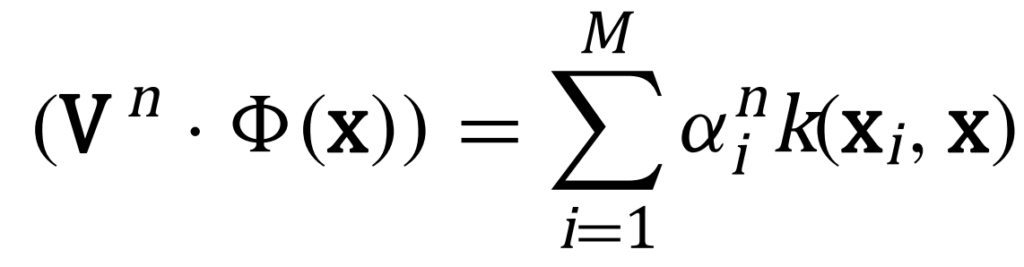
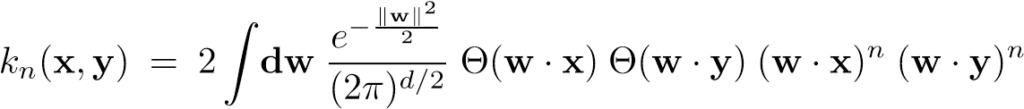
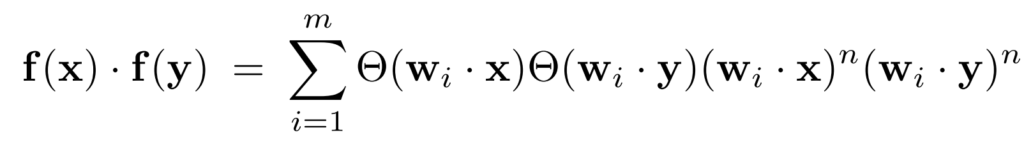
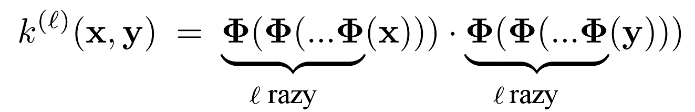




 polski
polski




























 English
English